Primeira e segunda derivada

Extremos e primeira derivada


Podemos utilizar a primeira derivada de uma função para determinar se uma função é crescente ou decrescente num intervalo.
Seja f uma função que admite primeira derivada num intervalo aberto I:

• f'(x)>0,f é crescente em I
• f'(x)<0,f é decrescente em I
• f'(x)=0,f é constante em I

Nos pontos onde a função passa de crescente para decrescente ou vice versa, a função tem um extremo relativo. Os extremos relativos de uma função, incluem os mínimos relativos e os máximos relativos da função.

Se f tem um mínimo ou um máximo relativo em x=c, então ou f'(x)=0 ou f'(x)não esta definido.

Concavidade e a segunda derivada

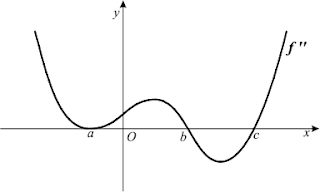
Podemos utilizar a segunda derivada da função para determinar os intervalos em que as concavidades do gráfico estão voltadas para cima ou para baixo.

Seja f uma função que admite segunda derivada num intervalo aberto I:

• f''(x)>0,f tem concavidade voltada para cima em I
• f'(x)<0,f tem concavidade voltada para baixo em I

Para uma função f contínua, podemos calcular os intervalos em que f tem concavidade voltada para cima ou para baixo. (Para uma função descontínua, os intervalos de teste devem ser formados utilizando-se os pontos de descontinuidade juntamente com os pontos em que f’’ (x) é zero ou é não definida.